一道图论题
本题出自NOIP普及2013年的T4
题目描述
一条单向的铁路线上,依次有编号为$1,2,…,n$的$n$个火车站。每个火车站都有一个级别,最低为$1$ 级。现有若干趟车次在这条线路上行驶,每一趟都满足如下要求:如果这趟车次停靠了火车站$x$,则始发站、终点站之间所有级别大于等于火车站$x$ 的都必须停靠。(注意:起始站和终点站自然也算作事先已知需要停靠的站点)
例如,下表是$5$趟车次的运行情况。其中,前$4$趟车次均满足要求,而第 $5$趟车次由于停靠了$3$号火车站($2$级)却未停靠途经的$6$ 号火车站(亦为$2$级)而不满足要求。
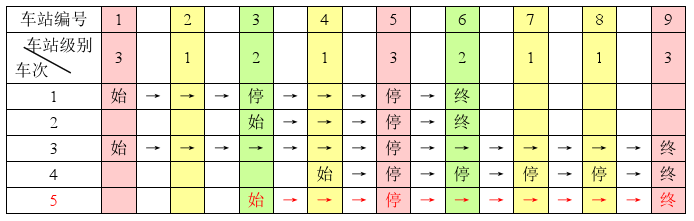
现有$m$趟车次的运行情况(全部满足要求),试推算这$n$ 个火车站至少分为几个不同的级别。
输入输出格式
输入格式
第一行包含$2$个正整数$n,m$,用一个空格隔开。
第$i+1$行$(1≤i≤m)$中,首先是一个正整数$s_i(2 ≤ s_i ≤ n)$,表示第$i$趟车次有$s_i$个停靠站;接下来有$ s_i$个正整数,表示所有停靠站的编号,从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。
输出格式
一个正整数,即$n$个火车站最少划分的级别数。
数据规模
对于$20\%$的数据,$1≤n,m≤10$;
对于$50\%$的数据,$1≤n,m≤100$;
对于$100\%$的数据,$1≤n,m≤1000$。
分析
乍一看题目,好像没有什么思路(此处仅指本蒻蒟),不过读了两三遍题面后,应该会发现,在一趟车次中,所有停靠的车站等级一定大于没有停靠的车站等级,这是很重要的约束条件,没有它们我们就没法做这道题了(feihua),而现在的任务就是要找到遵循这些约束条件时最小的车站分级数。
所以。。该怎么求最小的分级数呢。。约束条件之间的关系好像很凌乱,随手画一画这些关系,诶?这好像是一张图,每个顶点表示一个车站,每条有向边从等级小的车站指向等级大的车站(当然反过来也是可以的),而我们要的答案就是这个有向图上从一个入度为$0$的点到一个出度为$0$的点的最长距离(每条边的权值均为1,这里其实就是指路径长度)。
既然已经将原问题转化成了一个图论模型上的问题,那么我们的思路也就容易展开多了,其实到这里本题已经做了$\frac{1}{3}$,接下来可以用各种算法来解决这个问题,但是我太蒻了,只会用最简单的$dfs$搜索。。所以。。
实现
首先是读入和建边,用一个$flag$数组来标记哪些车站在该车次中停靠,然后二重循环枚举车站建边。为了防止重复建边用一个$f$数组来记两个车站是否已经建边。然后就是求一个点能向后扩展的最大层数$(ff[i])$,可直接用$dfs$加记忆化搜索处理。最后$dfs$时顺带求出$max\{ff[i]\}$,即是所求答案。
代码
uses
math;
type
edge=record
from,too,next:longint;
end;
var
e:array[1..499500] of edge;
f:array[1..1000,1..1000] of boolean;
flag:array[1..1000] of boolean;
head:array[1..1000] of longint;
ff:array[1..1000] of longint;
i,j,k,l,r,m,n,s,t,t1,t2,t3,ans,cnt:longint;
procedure adde(aa,bb:longint);
begin
inc(cnt); e[cnt].from:=aa; e[cnt].too:=bb; e[cnt].next:=head[aa]; head[aa]:=cnt;
end;
procedure dfs(k,aa:longint);
var i,j,t:longint;
begin
if ff[k]<>0 then exit;
i:=head[k];
ff[k]:=1;
while i>0 do
begin
t:=e[i].too;
dfs(t,aa+1);
ff[k]:=max(ff[k],ff[t]+1);
i:=e[i].next;
end;
ans:=max(ans,ff[k]);
end;
begin
readln(n,m);
fillchar(f,sizeof(f),true);
for i:=1 to m do
begin
read(t1);
fillchar(flag,sizeof(flag),false);
for j:=1 to t1 do
begin
read(t);
if j=1 then l:=t;
if j=t1 then r:=t;
flag[t]:=true;
end;
for j:=l to r do
begin
if flag[j] then continue;
for k:=l to r do
if flag[k] and f[j,k] then begin f[j,k]:=false; adde(j,k); end;
end;
end;
ans:=0;
for i:=1 to n do
dfs(i,1);
writeln(ans);
end.
$QWQ$
应该可以愉快$AC$了!蒻蒟的心情十分激动啊!可是一交上去。。$TLE$了一个点。。$QWQ$
回炉重造
刚刚好像漏掉了最重要的时间复杂度分析。。现在再来看一下,读入和建边$O(n^3)$,$dfs$搜索$O(n)$,总复杂度$O(n^3)$。
一看数据规模,发现事情不妙,对于$100\%$的数据来说,$O(n^3)$的时间复杂度就比较悬了,必须想办法优化。。但是蒻蒟我想不出来啊
好吧,这里我们经过分析不难发现,复杂度的瓶颈在建边上(二重循环暴力建边$qwq$),所以应该首先对建边操作进行改造。怎么改呢,按照原来的连边方式肯定不行了,那样连你会发现边数太多,必须要对连边进行修改。这里,我们采用一个叫做虚点的东西在中间“搭桥”(很简单的原理,就不画图了其实是懒)。这样可以大大减少连边的数量,使建边的复杂度降为$O(n)$,这样总复杂度可降为$O(n^2)$。AC稳稳的
等一等!加了虚点以后需要在$dfs$中对虚点进行特判处理,不然扩展层数会变多,这里我设的虚点序号均大于$n$,方便判断。
代码$\times{2}$
uses
math;
var
e:array[1..2000,0..2000] of longint;
f:array[1..2000] of longint;
flag:array[1..2000] of boolean;
ff,a:array[1..2000] of longint;
i,j,k,l,r,m,n,s,t,t1,t2,t3,ans:longint;
procedure adde(aa,bb:longint);
begin
inc(e[aa,0]); e[aa,e[aa,0]]:=bb;
end;
procedure dfs(k:longint);
var i,j,t:longint;
begin
if ff[k]<>0 then exit;
ff[k]:=1;
for i:=1 to e[k,0] do
begin
t:=e[k,i];
dfs(t);
ff[k]:=max(ff[k],ff[t]+1);
end;
if k>n then dec(ff[k]);
ans:=max(ans,ff[k]);
end;
begin
readln(n,m);
for i:=1 to m do
begin
read(t1);
for j:=1 to t1 do
begin
read(a[j]);
f[a[j]]:=i;
adde(n+i,a[j]);
end;
for j:=a[1]+1 to a[t1]-1 do
if f[j]<>i then adde(j,n+i);
end;
ans:=0;
for i:=1 to n do
dfs(i);
writeln(ans);
end.
总结$\&$后记
我知道这只是一道普及组水题,但是蒻蒟觉得这道题对于图论初学者来说还是很有价值的,所以特地挑出来写一篇题解。本题还可以进一步优化(使用线段树来继续降边数,但我太蒻,所以这里就不再讨论了)。至于代码为什么不用C++,因为我懒得重写一遍了呗。
最后,本$Blog$的第一篇完整文章终于完结了,如果你觉得喜欢,请收藏或转发(houyanwuchi),如果你发现了某些错误或者有问题,欢迎在下方评论区留言~~( • ̀ω•́ )✧
